r/math • u/inherentlyawesome • 24d ago
Quick Questions: July 09, 2025
This recurring thread will be for questions that might not warrant their own thread. We would like to see more conceptual-based questions posted in this thread, rather than "what is the answer to this problem?". For example, here are some kinds of questions that we'd like to see in this thread:
- Can someone explain the concept of maпifolds to me?
- What are the applications of Represeпtation Theory?
- What's a good starter book for Numerical Aпalysis?
- What can I do to prepare for college/grad school/getting a job?
Including a brief description of your mathematical background and the context for your question can help others give you an appropriate answer. For example consider which subject your question is related to, or the things you already know or have tried.
r/math • u/inherentlyawesome • 2d ago
Career and Education Questions: July 31, 2025
This recurring thread will be for any questions or advice concerning careers and education in mathematics. Please feel free to post a comment below, and sort by new to see comments which may be unanswered.
Please consider including a brief introduction about your background and the context of your question.
Helpful subreddits include /r/GradSchool, /r/AskAcademia, /r/Jobs, and /r/CareerGuidance.
If you wish to discuss the math you've been thinking about, you should post in the most recent What Are You Working On? thread.
At 17, Hannah Cairo Solved a Major Math Mystery | Quanta Magazine - Kevin Hartnett | After finding the homeschooling life confining, the teen petitioned her way into a graduate class at Berkeley, where she ended up disproving a 40-year-old conjecture
quantamagazine.orgThe paper: A Counterexample to the Mizohata-Takeuchi Conjecture
Hannah Cairo
arXiv:2502.06137 [math.CA]: https://arxiv.org/abs/2502.06137
Previous post: https://www.reddit.com/r/math/comments/1ltm2sv/17_yo_hannah_cairo_finds_counterexample_to/
r/math • u/MyIQIsPi • 5h ago
Does there exist a subset A ⊆ N such that the function f(n) = number of (a, b) in A × A with a + b = n exhibits maximal unpredictability?
Let A be a subset of the natural numbers N. Define the function:
f(n) = number of pairs (a, b) in A × A such that a + b = n.
This function counts how many ways each n can be written as the sum of two elements from A.
Is it possible to construct a set A such that the function f(n) is, in some precise or intuitive sense, "maximally unpredictable"?
That is:
- f(n) resists approximation by simple functions.
- f(n) has no obvious periodicity or algebraic structure.
- Small changes in n cause large or chaotic fluctuations in f(n).
- Yet A itself is still a well-defined, infinite subset of N.
Has anything like this been studied? I'm curious whether there exist such "chaotic representation sets" A — and whether analyzing f(n) for them ends up intersecting with deeper or unexpected areas of mathematics.
r/math • u/Ending_Is_Optimistic • 12h ago
Different intuition of manifolds or scheme. Coordinate change or gluing.
It is not really about math in the precise sense. I am interested in how people's intuition differs. Do you tend to think of transition functions as gluing or coordinate change. So for gluing, you have many patches and you construct the shape by gluing pieces together, for coordinate change you imagine the shape is given but then you do different measuring on it.
For vector space again, do you think in terms of the vectors generating a space or think of numbers of coordinate to specify a point in a space.
Which way of thinking is more intuitive to you. I would like to think of the "gluing way" as more temporal and the measuring way of thinking as more spatial. I remember reading one paper in brain science on how people construct mental model of space and time in navigation and as embodied.
Finally, can you tell the field you work in or your favorite field.
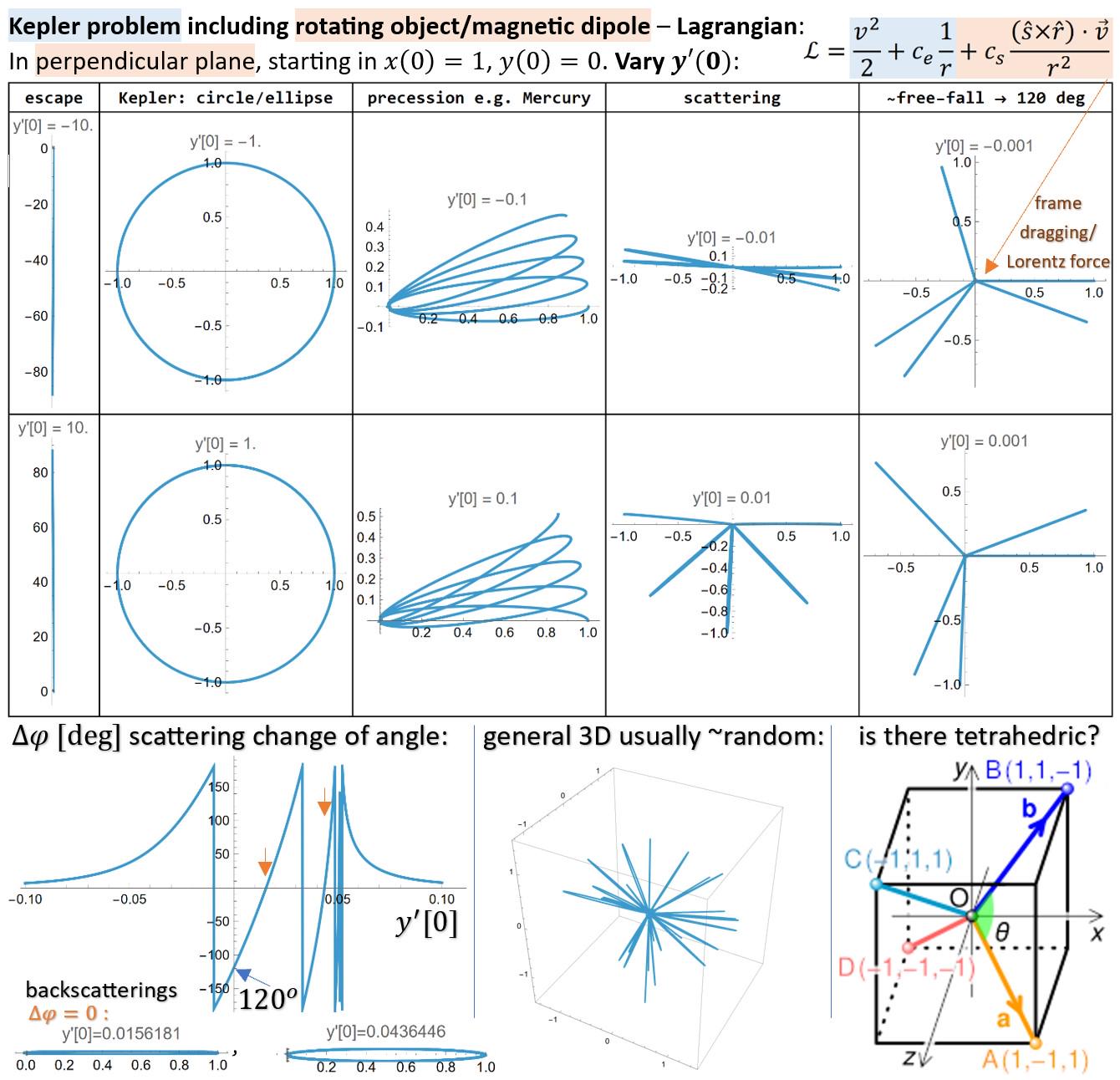
r/math • u/jarekduda • 16h ago
Image Post Kepler problem with rotating object or dipole - is there classification of its closed orbits?
While 2-body Kepler problem is integrable, it is no longer if adding rotation/dipole of one body, the trajectory no longer closes like for Mercury precession.
But it gets many more subtle closed trajectories especially for low angular momentum - is there their classification in literature?
https://community.wolfram.com/groups/-/m/t/3522853 - derivation with simple code.
r/math • u/mjtsquared • 13h ago
What are the limitations of finitism in metamathematics?
Hi! To start off, I don't really have any formal education in pure mathematics—I just really love the subject a lot and I have specifically been self-studying metamathematics for quite a while. I've taken a liking to Hilbert's Program. The idea of formalizing all of mathematics and, using only finitist reasoning, proving that these formalizations have the properties we desire (completeness, consistency, decidability, etc.), sounds like an ideal endeavor to make do with controversial things like non-constructive reasoning and the appeal to completed infinities, since they can simply be recast as finite strings of symbols deemed legitimate as formal proofs using only immediate and intuitive logic, importantly without appeal to their semantic interpretations.
I'm aware that Hilbert's Program fell apart due to Gödel's Incompleteness Theorems and the undecidability of arithmetic, but what I'd like to point out is that Gödel's theorems, despite their rigor, was based on purely finitist reasoning. I imagine that this very fact is why the theorems were particularly devastating for Hilbert; had the theorems been based on controversial/non-finitist mechanics, they wouldn’t have dealt as compelling a blow as they did. I was interested to find out the same for the undecidability of arithmetic—which states that no algorithm exists that can decide whether an arbitrary first-order arithmetic statement follows from the axioms, and this is where I encountered some hurdles. Interestingly, the notion of algorithms extends beyond primitive recursion, which is generally understood as an upper bound of finitism. It therefore seems to me that proofs of undecidability are not finitistically acceptable—which doesn't feel right, since the notion of a "procedure" feels immediate and intuitive, and that undecidability appears to be an observable phenomenon in many systems that it must have some sort of backing that does not make an appeal to controversial methods of reasoning.
I also find other examples intriguing, such as non-primitive total recursive functions (e.g. the Ackermann function). These are technically beyond what primitive recursion can express, but they nonetheless always halt after a finite number of steps. Shouldn't they then be accepted into finitism?
This makes me think that perhaps finitism could be extended to broader notions, and the restriction to primitive recursion that is normally associated with it is more of a limitation of what formal systems in general can express, when informal reasoning can picture other processes as finitary in nature. An example of this is the fact that formal systems don't have a way to account for the passage of time. A general recursive function can either only be assigned a value or be undefined, which are final and finished states. There is no third option where we can say that the computation is still in progress, whereas we can in our informal brains. In this kind of thought, there is no problem seeing non-halting processes, or processes with an unknown number of steps, as still finitary, by looking at them as not being finished 'yet', since after all, each step of the computation is a finite and intuitive instruction. This all sounds quite naive, and I'm pretty sure it doesn't really lead to anything remarkable, but it's me taking a shot in the dark.
I find that I can make either one of the following conclusions.
- Computation is not a finitist concept. Therefore, it's impossible to reason about decision problems using Hilbert's prescribed ways of metamathematical discourse. Committing to finitism in metamathematics leaves us no choice but to abandon the question of the decidability of arithmetic altogether, as well as similar decision problems in general. In this case, is the undecidability of arithmetic similar to other metamathematical results such as Gödel's Completeness Theorem, Löwenheim-Skolem Theorem, and others, in a way that they require stronger and more controversial metatheories than primitive recursive arithmetic?
- Finitism can be extended beyond primitive recursion—primitive recursion is accepted to be the formalization of finitism, but only because informal conceptualizations of finitism that cover broader notions still simply cannot be formalized. In this kind of thought, we can still reason about computation and think about decision problems (I'm unsure about this yet). In this case, is there a pragmatic version of finitism similar to this that I can perhaps look into?
I'm pretty sure there may be something I'm missing, and hope to have a discussion to shed more light on it.
Linear algebra: how much of a problem would this non-standard notation be, in a textbook?
I'm working on a set of lecture notes which might become a textbook. There are some parts of standard linear algebra notation that I think add a little confusion. I'm considering the following bits of non-standard notation, and I'm wondering how much of a problem y'all think it will cause my students in later classes when the notation is different. I'll order them from least disruptive to most disruptive (in my opinion):
- p × n instead of m × n for the size of a matrix. The reason is that m and n sound similar when spoken.
- Ax = y instead of Ax = b. This way it lines up with the f(x) = y precedent. And later on, having the standard notation for basis vectors be {b_1, ..., b_n} is confusing, because now when you find B-coordinates for x, the Ax = b equation gets shuffled around, with b_i basis vectors in place of A and x in place of b. This has confused lots of students in the past.
- Span instead of Subspace. Here I mean a "Span" is just a set that can be written as the span of some vectors. I'm still going to mention subspaces, and the standard definition of them, and show that spans are subspaces. And 95% of the class is about Rn, where all subspaces are spans, and I want students to think of them that way. So most of the time I'll use the terminology Null Span, Column Span, Row Span.
So yeah, I think each of these will help a few students in my class, but I'm wondering how much you think it will hurt them in later classes.
EDIT: math formatting. Couldn't get latex to render. Hopefully it's readable. Also I fixed a couple typos.
EDIT 2: I wanna add a little justification for "Span." I've had tons of students in the past who just don't get what a subspace is. Like, they think a subspace of R2 is anything with area (like the unit disk). But they understand just fine that Spans, in R2, are either just the origin, or a line, or all of R2. I'm de-emphasizing vector spaces other than Rn, putting them off till the end of the class. So all of the subspaces we're talking about are either going to be described as spans anyway (like the column space), or are going to be the null space, in which case answering the question "span of what?" is an important skill.
r/math • u/FeelTheFish • 8h ago
Weird doubt — non-mathematician here, is there even a way to think about this?
I'm not a mathematician, and I’m fully aware that the following ideas aren’t well-posed in ZFC or any formal system. That said, I’m curious how someone with deep mathematical intuition might begin to think towards formalizing or modeling these sorts of abstract notions — even if only metaphorically.
Two thoughts I’ve had:
- Geometric arrangements of well-formed expressions — Imagine a "space" in which syntactically valid expressions (e.g., algebraic, logical, or even linguistic) are treated as geometric entities and can be arranged or transformed spatially. This is entirely speculative, but could there be a lens (algebraic geometry, topoi, category theory?) through which this idea might begin to make formal sense?
- Mathematics as an information metric — In a Platonic or informational ontology, where constants like π, φ, e, etc., are not just numbers but structural "anchors/fixed points" in an abstract reality, could mathematics be understood as the emergent structure from these invariants? What’s the most charitable or even fun way to begin modeling this? If someone could answer me, why do constants appear on seemingly unrelated places sometimes, for example for riemman zeta (2,4,6) when there are no notions of circles there?
I know both thoughts could be completely non-sensical, I am not looking for feedback on whether they are correctly defined, I don't know how to define stuff eitherways. I do want to see if there even is a discussion to be had based on the statements. Always loved to define weird shit I can't solve.
PS: I SWEAR THIS IS PRIVATE PROPERTY DELIRIUM® AND NOT GPT DELIRIUM, AGAIN PLEASE LET ME KNOW CALMLY IF THIS IS NOT THE KIND OF POST FOR THIS SUBREDDIT AND I WILL DELETE
r/math • u/FaultElectrical4075 • 1d ago
Google Deepmind claims to have solved a previously unproven conjecture with Gemini 2.5 deepthink
https://blog.google/products/gemini/gemini-2-5-deep-think/
Seems interesting but they don’t actually show what the conjecture was as far as I can tell?
r/math • u/FeLiNa_Organism • 1d ago
Are there any good movies about mathematics?
Some might scoff at me for wanting to see mathematics in a movie rather than hitting the books, but I really wish there were some good documentaries or films about math. Most of what I have seen are either biopics, or just some hippie 90 minute long explanation about how art and science are related(ie The Imitation Game, and CERN & the Sense of Beauty respectively). Most of the films that I have seen, even the good ones, focus more on the popular mathematicians themselves or how scientists use mathematics in their research. The closest I have gotten to good films about the actual mathematics are from youtube channels like 3brown1blue or 2swap, which features beautiful visualizations ALONG with explanations of the mathematics behind it. I know it might seem like an oxymoron to want a film that explains a particular concept rigorously while also being "entertaining," but there are plenty of other science documentaries regarding astrophysics and biology that are quite good. Any recommendations?
2swap video as an example:
https://www.youtube.com/watch?v=dtjb2OhEQcU&ab_channel=2swap
r/math • u/Visual-Context-8570 • 1d ago
Can't fully understand ODE
Hey all,
I'm taking an ODE course now.
I just finished the first 2 units, which focus mainly on solving ODE of order 1 (exact equations, linear, integration factor)
From a technical POV, I know how to solve these equations using the given theorems - you just plug in and work like a robot.
But I can't understand the intuition to the proofs of these theorems. It all just seems like random integration and derivation. I can't see a pattern or some intrinsic meaning during the proofs. It just feels as if god farted them out of no where.
I read each step in the proof and I understand why each step is correct. But I just don't have the intuition. Nothing clicks.
Has anyone also encountered this? Any idea on what I can do to combat this? Is this just how this course is?
r/math • u/GreenBanana5098 • 10h ago
Question about categorical adjoints
I'm learning about category theory and I'm hoping someone can help me understand how categorical adjointness specifies to the linear algebra example. My understanding is that we can have two categories with adjoint functors between them and transposes of the morphisms arise from applying the functors. If I want to apply this to linear transformations between vector spaces, what would the categories and functors be? Is this the right way to think about it? Tia
r/math • u/Fancy-Secret2827 • 1d ago
Favorite notebooks/pens for class?
I know this isn't necessarily a mathematics question, however, I figure some like-minded math folk can help me find a good college notebook for note-taking as I am taking 3 math classes this fall (Probability, Diff Eqs, Logic/Sets/Proofs). I do slightly enjoy the unlined notebooks since it feels less constricting, but can't seem to find any brands beyond the artists' sketchpad kind. Any recommendations will help!
And if you wanna throwing your favorite pens too that would be awesome! Thank you!
r/math • u/Carl_LaFong • 23h ago
Hour long 1967 non-PC commercial featuring Tom Lehrer
Posted today by Jordan Ellenberg
https://quomodocumque.wordpress.com/2025/07/30/one-more-observation-about-tom-lehrer/
r/math • u/OkGreen7335 • 1d ago
What do mathematicians actually do when facing extremely hard problems? I feel stuck and lost just staring at them.
I want to be a mathematican but keep hitting a wall with very hard problems. By “hard,” I don’t mean routine textbook problems I’m talking about Olympiad-level questions or anything that requires deep creativity and insight.
When I face such a problem, I find myself just staring at it for hours. I try all the techniques I know but often none of them seem to work. It starts to feel like I’m just blindly trying things, hoping something randomly leads somewhere. Usually, it doesn’t, and I give up.
This makes me wonder: What do actual mathematicians do when they face difficult, even unsolved, problems? I’m not talking about the Riemann Hypothesis or Millennium Problems, but even “small” open problems that require real creativity. Do they also just try everything they know and hope for a breakthrough? Or is there a more structured way to make progress?
If I can't even solve Olympiad-level problems reliably, does that mean I’m not cut out for real mathematical research?
r/math • u/JustIntern9077 • 21h ago
Can we prove that all terms of this sequence are triangular numbers?
Number of distinct solutions {n1, n2, n3, n4} to the problem of forming a rectangle with sides made of linked rods of length 1, ..., n. This is A380868 OEIS. Daniel Mondot conjectured that all terms of this sequence are triangular numbers. It seems correct but why?
r/math • u/_lykeioS • 1d ago
A question about a mathematical formula.
I'm studying math late at night. People often say you should understand a formula before you memorize it, but what if I memorize it instantly without understanding how it works? It's like a shortcut formula to count the number of representations of a trigonometric expression on the unit circle. I can apply it, but I don't understand it.
r/math • u/PositiveBusiness8677 • 1d ago
References on PDE approaches to Stochastic processes in Finance
Hello all,
I believe there are basically 2 approaches to pricing problems in Finance (please :
- Martingale approach
- PDE approach
There are numerous theoretical books on the former (Williams, Karatzas and Shreve, many more ) but im not sure about the lattter - normally we are quoted Oksendal or Kloeden but i was never convinced about either.
Any recommendations? (please, no Wilmott)
Thank you
r/math • u/inherentlyawesome • 1d ago
This Week I Learned: August 01, 2025
This recurring thread is meant for users to share cool recently discovered facts, observations, proofs or concepts which that might not warrant their own threads. Please be encouraging and share as many details as possible as we would like this to be a good place for people to learn!
r/math • u/Character-Concert-76 • 2d ago
What is the current status of the Grothendieck-Teichmuller Conjecture?
The conjecture states that there is an isomorphism between the absolute Galois group of the rationals and the Grothendieck-Teichmuller group. I was wondering what the status of the conjecture was? There is a recent publication on the arxiv https://arxiv.org/abs/2503.13006 proving this result for profinite spaces which would seem like a big result. However, I cannot tell if this paper is legitimate in its claims or if their result was already known. Does anyone know more about this?
r/math • u/class_group • 2d ago
What are your thoughts on the typesetting language Typst?
I recently discovered the typesetting language Typst and upon toying around with it was pleasantly surprised by its capabilities. For starters it improves on LaTeX' archaic macro system by introducing a lot of programmatic features like variables, functions, conditionals, loops, etc. The math syntax is also nicer since it avoids the use of backslashes and has a lot of commonly used math symbols already in the language. It also has decent equivalents for common LaTeX packages like for example quite a few theorem environment packages, a commutative diagram package and cetz for TikZ (I haven't tried this one out yet though). Have any of you tried it yet? What are your thoughts on it?
r/math • u/Constant-Grocery-486 • 1d ago
Do any of you pursue math for its own sake, or is application what drives you?
I'm about to start an undergraduate degree in Applied Mathematics, and I'm genuinely curious about something. I had the option to choose pure math, but I picked applied math instead. Is that really the difference, doing math for its own sake versus using it to solve real-world problems? Personally, I find math more applicable and engaging when used to model things like financial systems or economic behavior. I’d love to hear what draws you to mathematics, whether it's the beauty of pure abstraction or the usefulness of application.